Pour financer leurs investissements, les grandes sociétés peuvent faire appel au marché financier. L’emprunt obligataire est un emprunt à moyen ou à long terme contracté par une société auprès de plusieurs prêteurs, le plus souvent de grandes banques. Cet emprunt est divisé en parts égales appelées obligations remboursables selon diverses modalités possibles.
Chaque obligataire est titulaire de droits :
droit à la perception d’un intérêt annuel ou coupon calculé sur la valeur nominale du titre à l’aide d’un taux d’intérêt nominal,
droit au remboursement de l’obligation en numéraire ou en actions à une date d’échéance.
Caractéristiques des emprunts obligataires
Valeur nominale
Elle sert de base pour le calcul des intérêts .
La valeur est identique pour toutes les obligations d’un même emprunt.
Elle est comprise en général, entre 200 E et 3000 E.
Prix d’émission
Il correspond au prix payé par l’obligataire.
Lorsque le prix d’émission est égal à la valeur nominale , l’emission est dite « au pair »
Le prix d’émission peut être inférieur à la valeur nominale. L’emission est dite « au dessous du pair ». La différence constitue une prime d’émission.
Donc :
Prime d’émission = Valeur nominale – Prix d’émission
Prix de remboursement
C’est le prix payé par la société, à l’échéance, aux différents obligataires.
Au pair
L’obligation peut être remboursée à la valeur nominale ou « au pair ».
Donc :
Prix de remboursement = Prix d’émission
Au dessus du pair
Elle peut être remboursée à un prix supérieur à la valeur nominale ou « au dessus du pair ».
Alors :
Prix de remboursement > à la valeur nominale
La différence constitue la prime de remboursement .
Donc :
Prime de remboursement = Prix de remboursement – Va leur nominale
Double prime
Lorsque le prix d’émission a été inférieur à la valeur nominale et que le prix de remboursement est supérieur à la valeur nominale il y a double prime:
Prime d’émission = Valeur nominale – Prix d’émission
et
Prime de remboursement = Prix de remboursement – Valeur nominale
alors
Double prime
ou
Double prime = Prix de remboursement – Prix d’émission
Amortissement des primes de remboursement.
Les primes de remboursement des obligations font l’objet d’un amortissement sur la durée de l’emprunt selon deux modalités :
Il existe deux modalités d’amortissement des primes de remboursement des obligations :
• soit au prorata de la durée de l’emprunt, par fractions égales
Dotation de l’exercice = Prime de remboursement / durée de l’emprunt
• soit au prorata des intérêts courus
Dotation = Prime x (Intérêts courus de l’exercice / Total des intérêts de l’emprunt)
Frais d’émission.
Il s’agit des frais engagés lors de l’émission de l’emprunt obligataire :
frais de publicité pour les parutions d’annonces légales pour les emprunts émis par de grandes sociétés et nécessitant un appel public à l’épargne.
commissions des intermédiaires financiers.
Ils peuvent être :
soient maintenus en charges pour la totalité dans l’exercice de leur engagement,
soient activés et transférés en charges à répartir sur plusieurs exercices en vue de leur étalement par amortissement.
Modalités du remboursement.
Principes.
Le plus souvent, les emprunts obligataires sont remboursables en totalité « in fine ».
Cependant, ils peuvent être remboursés selon un plan d’amortissement d’emprunt :
soit par amortissements constants.
soit par annuités constantes.
Quelle que soit la solution utilisée, le nombre d’obligations remboursées ou « amorties » est égal au rapport :
Montant global du remboursement (amortissement) / prix de remboursement.unitaire
Les obligations non amorties sont dites « vivantes ».
En totalité IN FINE.
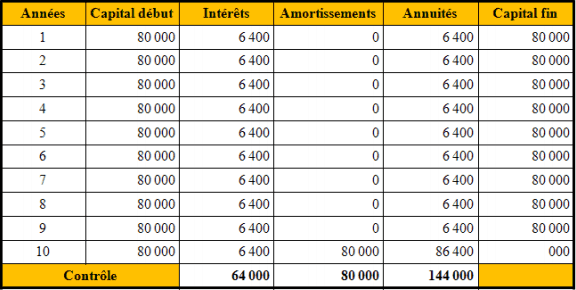
1°) Méthode : Le remboursement est effectué « en bloc » à la fin de la durée de l’emprunt. 2°) Exemple :
• Montant de l’emprunt : 80 000 € ;
• Durée : 10 ans ;
• Taux : 8 % ;
• Prix de remboursement : 500 € par obligation ;
• Nombre d’obligations amorties : 80 000 / 500 = 160
Amortissement constant.
1°) Méthode :
Amortissement (remboursement) = (C x N) / n
avec : C : valeur nominale de l’obligation
N : nombre d’obligations
n : durée de l’emprunt
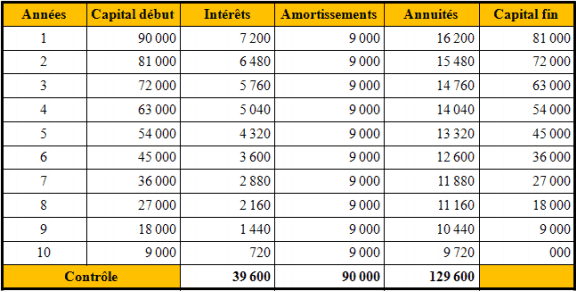
2°) Exemple :
• Montant de l’emprunt : 90 000 € ;
• Durée : 10 ans ;
• Taux : 8 % ;
• Prix de remboursement : 100 € par obligation ;
• Remboursement annuel : 9 000 € ;
• Nombre annuel d’obligations amorties : 9 000 / 100 = 90.
Annuités Constantes.
1°) Méthode :
a = C x N x t / 1 – (1 + t) -n
avec : a : annuité
C : valeur nominale
N : nombre d’obligations
t : taux d’intérêt
n : nombre d’annuité
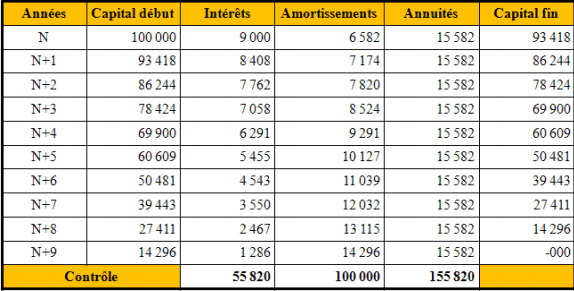
2°) Exemple :
• Montant de l’emprunt : 100 000 € ;
• Durée : 10 ans ;
• Taux : 9 % ;
• Annuité : 15 582 €
• Prix de remboursement : 100 € par obligation ;
• Amortissement en N+8 : 13 115 € ;
• Nombre d’obligations amorties en N+8 : 131.
Traitement comptable des emprunts obligataires
Frais d’émission.
Les entreprises ont le choix entre :
Déduction immédiate.
La totalité des frais d’émission peut être déduite dès l’exercice de leur engagement :
Étalement.
La charge peut être étalée sur une durée équivalente à celle de l’emprunt par fractions égales ou au prorata des intérêts courus. L’étalement des charges à répartir se fait alors par la technique de l’amortissement direct dans le compte 481. « Charges à répartir sur plusieurs exercices », compte de bilan.
Écritures à la fin de l’exercice :
Primes de remboursement.
Calcul.
La différence entre le prix de remboursement et le prix d’émission, la prime d’émission globale pour l’ensemble des titres est enregistrée au débit du compte 169 Primes de remboursement des obligations.
Ce compte figure à l’actif du bilan parmi les comptes de régularisations et fonctionne selon la technique de l’amortissement direct.
Traitements comptables.
Ecriture lors de l’émission de l’emprunt obligataire :
Les primes de remboursement des obligations doivent être amorties sur la durée de l’emprunt. A la fin de chaque exercice comptable, pendant toute la durée de l’emprunt :
Intérêts courus
Calcul
A la clôture de chaque exercice comptable, en raison des principes comptables de rattachement des charges et d’indépendance des exercices, il est nécessaire d’évaluer les intérêts courus non échus sur les emprunts (I.C.N.E.).
I.C.N.E. de l’exercice = Valeur nominale de l’emprunt restant dû x Taux d’intérêt x Prorata (n/360)
Traitements comptables
Remarque :Les I.C.N.E. sont rattachés aux emprunts obligataires et donc inclus dans la rubrique « Emprunts obligataires » au passif du bilan.
Bilan de l’emprunteur
Comptabilité du prêteur
Un prêt à moyen ou long terme constitue un emploi stable.
C’est une créance immobilisée incluse dans les immobilisations financières.
Accord du prêt
Le prêt accordé à un débiteur est ainsi enregistré :
Perception des intérêts
Les intérêts perçus constituent des produits financiers :
Remboursement du prêt
Le remboursement du prêt constitue une diminution de créance immobilisée :
Encaissement d’une annuité
L’encaissement d’une annuité comprend : une part d’intérêts et une part de remboursement :
Intérêts courus non échus
En fin d’exercice, les Intérêts Courus Non Échus sur les prêts doivent être évalués d’où l’écriture :
Le compte 2748 sera soldé par contre passation à l’ouverture de l’exercice suivant.
Emprunts obligataires :différents taux
Taux nominal
Taux d’intérêt annuel appliqué sur la valeur nominale de l’obligation.
Deux taux périodiques sont dits équivalents lorsqu’ils produisent des valeurs acquises égales dans le système des intérêts composés.
Exemple 1:
Taux de 6 % l’an.
Valeur nominale d’une obligation : 1 000 €.
Le taux équivalent mensuel est de 0,487 % :
• Valeur acquise selon taux annuel : 1000 x 1,06 = 1060
• Valeur acquise selon taux mensuel équivalent : 1000 x 1,00487¹² = 1060
• Le taux de 6 % annuel est équivalent au taux mensuel de 0,487 %.
Exemple 2:
Quel est le taux mensuel équivalent au taux annuel de 8 % ?
C x 1,08 n = C x (1 + tm) ¹²n
1,08 = (1 + tm) 12
1,08 1/12 = 1 + tm
tm =1,08 1/12 – 1 = 1,006434 – 1 = 0,006434
Le taux mensuel équivalent au taux annuel de 8 % est 0,6434 %.
Généralisation :
Taux effectif.
Le taux effectif d’un emprunt est le taux de revient réel. Il permet de réaliser l’équivalence entre le montant de l’emprunt et les sommes versées par l’emprunteur : intérêts, commissions et frais. Une fonction financière du tableur permet l’automatisation du calcul.
Exemple:
Emprunt 60 000 € :
• Taux nominal 8,5 %.
• Remboursement par annuité constante sur 6 ans.
• Commissions et frais : 1,5 % du montant de l’emprunt soit : 900 €.
Taux actuariel
Le taux actuariel est le taux de rendement réel de l ‘emprunt. Il permet de réaliser l’équivalence entre le prix d’émission de l’emprunt obligataire et les sommes reçues par l’obligataire. Une fonction financière de tableur permet l’automatisation du calcul.
Exemple:
Emprunt obligataire :
• Valeur nominale : 800 €.
• Prix d’émission : 795 €.
• Prix de remboursement in fine : 810 €.
• Durée 8 ans.
• Taux nominal : 7 %.
je veux des sujets du BAC G2 etude de cas
lorsqu’on parle de produit de l’emprunt dequois’agit il?
je voudrais un cas de rachat par l’entreprise de ses propres obligations