Calculs d’emprunt bancaire

Le calcul d’un emprunt bancaire permet de déterminer les éléments clés d’un crédit : mensualité, coût total, capital emprunté, durée, etc. Un tableau d’amortissement des emprunts ou d’amortissement financier c’est un plan de remboursement d’un emprunt par le moyen de décaissements échelonnés.

Il permet de mettre en évidence, à toutes les échéances, la part de l’emprunt remboursé, l’emprunt restant à rembourser, le montant de l’intérêt et la mensualité (intérêt+ emprunt remboursé). Ces quatre éléments sont primordiaux pour toute comparaison d’offre et la prise d’une meilleure décision.

Le calcul d’un emprunt bancaire

Je mets à votre disposition : un tableau de calcul automatique des emprunts. Il vous permet de comparer facilement les différents offres sur le marché et de visualiser les différents éléments qui vous permettent de prendre votre décision d’emprunt.

Comment peut-on s’en servir ?

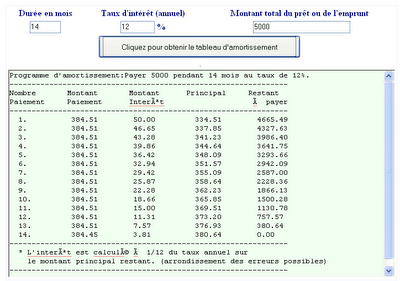
Je vous mets un exemple ci-dessous d’un emprunt de 5000 Euro au taux annuel de 12% à rembourser par 14 paiements mensuels. Une fois ces données introduites vous n’avez qu’à cliquer pour obtenir le tableau d’amortissement.

Dans le tableau vous aurez quatre colonnes principales que je vous explique ci-dessous en donnant comme exemple les calculs de la première ligne :

• Montant paiement : c’est la mensualité à payer = montant intérêt + part du capital à rembourser (principal). Pour la calculer, on a besoin d’une autre formule car la part du capital est inconnue pour le moment, donc pour la calculer nous avons une autre formule: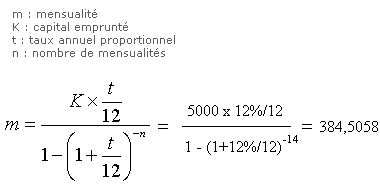Cette formule est celle appliquée au niveau des emprunts immobiliers, pourtant elle n’est pas la seul méthode de calcul de la mensualité
• Montant intérêt : c’est la part d’intérêt = Restant à payer x taux mensuel proportionnel = 5000 x 12%/12 = 50
• Principal : La part du capital à rembourser = mensualité – montant intérêt = 384,51 – 50 = 334,51
• Restant à payer : C’est ce qui reste à payer en déduisant les parts du capital déjà payées = 5000 – 334,51 = 4665,49

NB:

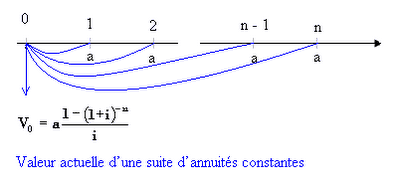
Le 1 dans la formule cité ici vient de la formule de la valeur actuelle d’une suite d’annuités (ou mensualités) qui devrait être égale au capital emprunté.

Si vous remplacez V0 par K, a par m et i par t/12 vous arrivez à la même formule cité dans cette article, qui provient de l’actualisation de chaque montant « a » à la période 0.

Pour le calculer dans une calculatrice, oui c’est possible et il faut apprendre à le faire en une seule fois pour arriver au résultat le plus juste possible.