Définition de la proposition logique : On appelle proposition tout énoncé susceptible de recevoir l’une des valeurs de la logique qui sont : la valeur « vrai » et la valeur « faux ». On exprimera cette bivalence par la table de vérité.
Table de vérité :
La table de vérité d’une proposition quelconque « p » se présente de la manière suivante :
- V et 1 désignent la valeur « vrai ».
- F et 0 désignent la valeur « faux ».
Le premier usage que l’on peut faire de ses tables est la construction d’une nouvelle proposition à partie d’une proposition donnée.
S’il y a deux propositions « p » et « q », on présente la table de vérité qui résume toutes les situations possibles de la façon suivante :
S’il y a trois propositions « p », « q » et « R » la table de vérité comportera huit lignes.
S’il y a « n » propositions, c’est à dire Q1 , Q2 , Q3 …. Qn , la table de vérité comportera 2n lignes.
A partie des tables de vérité, on peut construire des nouvelles propositions.
Négation :
La négation d’une proposition P est une proposition notée p (cette proposition se lie : non P) qui est vraie lorsque P est fausse et fausse lorsque P est vraie.
On peut également construire de nouvelles propositions à partir de deux
propositions P et Q. On parle de propositions logiques.
Composition logique : principe de correction :
A partir de deux propositions quelconques P et Q, de nouvelles propositions peuvent être construites. Ces propositions composées seront définies par leurs tables de vérité. Si on a deux propositions et deux valeurs alors quatre cas sont possibles :
La correction est l’opération qui permet de construire ces nouvelles constructions.
Différentes corrections de la logique :
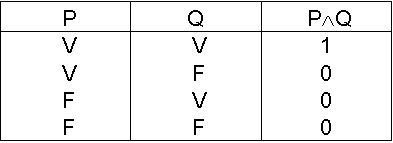
a- Conjonction : le signe 
(et).
La conjonction de deux propositions P et Q est une proposition notée PQ qui est vraie uniquement lorsque p et q sont vraies simultanément et fausses dans tous les autres cas.
b- Disjonction : le signe V (ou).
La disjonction de deux propositions P et Q est une proposition notée P V Q, qui est fausse si P et Q sont fausses simultanément et vraie dans tous les autres cas.
Lois de Morgon :
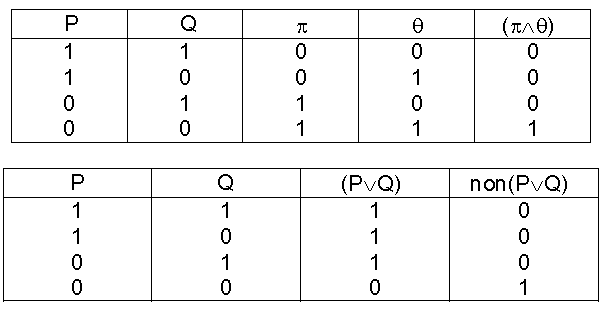
a- La négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions.
Ce résultat peut être vérifié à l’aide des tables de vérité :
b- 2ème cas de Morgan : la négation de la disjonction de deux propositions est équivalente à la conjonction des négations de deux propositions.
Ce résultat peut être vérifié à l’aide des tables de vérités.
Implication :
Si P et Q sont deux propositions, la proposition « si P alors Q » encore lue « P entraîne Q » est notée P ==> Q, et elle est appelée une implication. Elle est fausse uniquement si P est vraie et Q est fausse.
Négation de l’implication :
La négation de l’implication P==> Q est sous forme de 
.
Une implication et sa négation sont des propositions synonymes, c’est à dire q’elles sont en même temps vraies et en même temps fausses.
Réciproque :
La réciproque de l’implication P==> Q est la proposition Q ==> P.
Equivalence ou double implication :
L’équivalence de deux propositions P et Q est proposition notée P <==> Q, qui est vraie si P et Q ont la même valeur de vérité, et elle sera fausse dans les autres cas.
L’équivalence est synonyme de la proposition.
Loi logique :
Une loi logique est une proposition qui est toujours vraie quelque soit les valeurs de vérité des propositions qui la compose.
Exemple :
Laisser un commentaire