Clés de répartition en comptabilité analytique : règles générales de calcul

Les clés de répartition sont des données des problèmes proposés à la résolution des étudiants ; or dans la réalité il n’en est rien ! En effet, le comptable de l’entreprise qui doit calculer les coûts et les coûts de revient des produits et services de l’entreprise doit, en 1er lieu, déterminer les clés de répartition qu’il va utiliser pour répartir les frais des sections secondaires sur les sections primaires.

Personne ne vient lui poser un problème classique, tout fait, dans lequel les clés de répartition sont déjà données !

Car en fait, son vrai problème est justement de déterminer, d’abord les clés de répartition, base de ses calculs des coûts et des coûts de revient des produits et services de l’entreprise.

Après cette détermination des clés de répartition, son problème est à moitié résolu puisqu’il ne lui reste que des calculs classiques de problèmes classiques de comptabilité analytique.

Nous avons considéré, jusque là et à bon escient, que les clés de répartition sont des données des énoncés des problèmes que nous avons proposés et nous ne nous sommes pas posé de questions quant à leur valeur ou à leur signification ; nous allons exposer, dans ce qui suit, un ensemble de méthodes de calcul des clés de répartition et discuter, chaque fois, des valeurs, de la signification et de la portée de ces clés de répartition au niveau de la politique de l’entreprise.

Méthode de calcul des clés de répartition

On considère une entreprise constituée de plusieurs sections analytiques homogènes.

– SD : Section de Direction (administration et finance) ;
– SA : Section d’Achat ;
– SP : Section de Production ;
– SC : Section de Commercialisation.

Notons que les trois dernières sections sont des sections principales et que la 1ère section est une section auxiliaire dont il faut répartir les frais sur les 3 autres.

Cette répartition doit être faite selon des clés de répartition que nous ne connaissons pas et que personne n’est là pour nous les donner comme dans un problème classique de comptabilité analytique.

Voilà notre vrai problème de comptabilité analytique !

Règles générale de calcul des clés de répartition

La règle générale de calcul des clés de répartition, pour une entreprise, est que les frais indirects se répartissent, sur les différentes sections, proportionnellement à la « taille » de chaque section.

Ceci revient à dire que :

• Nous devons, d’abord, donner, dans chaque cas, une mesure de la « taille » d’une section analytique pour une entreprise ;
• Après quoi, nous devons répartir les frais indirects proportionnellement à cette mesure de la « taille » de la section.

Remarquons dès maintenant que cette mesure de la « taille » d’une section analytique n’a d’intérêt que du point de vue relatif d’une section par rapport aux autres sections.

Nous allons proposer dans ce qui suit un ensemble d’exemples de mesures de la « taille » d’une section analytique homogène, au sein d’une entreprise et nous discuterons ensuite de la pertinence de cette mesure et de son intérêt relativement à la politique de l’entreprise.

Mais faisons, dès maintenant une remarque sur les exemples qui vont suivre ; du fait qu’ils servent uniquement à exposer des méthodes de calculs, les chiffres qui y seront donnés n’ont aucune réalité, ils sont là, simplifiés, pour rendre nos calculs simples et notre exposé clair.

Première méthode de calcul des clés de répartition.

Considérons un cas particulier simple pour illustrer cette 1ère méthode.

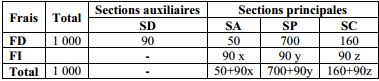
90, 50, 700 et 160 représentent les frais directs (FD) de chaque section.

90 représentent les frais directs de la section SD qui doivent être répartis sur les 3 autres sections SA, SP et SC et constituer les frais indirects (FI).

x, y et z sont les clés de répartition (en %) des frais indirects.
90 x, 90 y et 90 z sont les frais indirects des 3 sections SA, SP et SC et qui représentent la répartition des frais de la section SD.

On doit avoir x + y + z = 100 %  et 90 x + 90 y + 90 z = 90

Cette 1ère méthode est basée sur l’hypothèse que la « taille » d’une section analytique se mesure par la masse totale des frais qu’elle supporte.

Ainsi, dire que la « taille » d’une section, relativement aux sections, se mesure par la masse totale des frais qu’elle supporte a pour conséquence, quant au calcul des clés de répartition que les frais indirects se répartissent sur les différentes sections proportionnellement aux frais globaux que supporte chaque section.

Traduisons alors le fait que les frais indirects sont proportionnels aux frais globaux, de ces sections.

(90 x/50 + 90 x) = (90 y/700 + 90 y) = (90 z / 160 + 90 z)

Nous semblons, à ce stade, être bloqués du fait que ne connaissant pas les frais indirects de chaque section, il nous est difficile d’accéder aux frais globaux de cette section.

Nous pourrions lever cette difficulté en manipulant quelque peu les deux égalités établies ci-dessus mais nous préférons donner une assertion équivalente à notre postulat concernant la mesure de la « taille » d’une section analytique.

En effet, dire que les frais indirects se répartissent sur les différentes sections proportionnellement aux frais globaux de chaque section, est équivalent à dire que les frais indirects se répartissent sur les différentes sections proportionnellement aux frais directs seulement de chaque section.

Ainsi, dire que la « taille » d’une section analytique se mesure, relativement aux autres sections, par la masse totale des frais qu’elle supporte revient à dire que la « taille » d’une section analytique se mesure, relativement aux autres sections, par la masse des frais directs qu’elle supporte.

Ceci donne les 2 égalités simples suivantes :

(90 x/50) = (90 y/700 ) = (90 z / 160)

Ces deux dernières égalités donnent une 3ème.

(90 x/50) = (90 y/700) = (90 z / 160) = (90 x + 90 y + 90 z / 50 + 700 +160)= 90/910

Et de là, nous pouvons calculer x, y et z.

90x/50 = 90/910

Ce qui donne x = 5,49 %   et 90 x = 4,94

90y/700 = 90/910

Ce qui donne y = 76,92 %  et 90 y = 69,23

90z/160 = 90/910

Ce qui donne z = 17,58 %
et 90 z = 15,82
On trouve bien : x + y + z = 100 % et 90 x + 90 y + 90 z = 90

Cette 1ère méthode trouve sa justification dans le fait qu’il semble raisonnable, pour une entreprise, qu’on affecte à chaque section analytique une part des frais indirects proportionnellement à sa part dans la mesure totale des frais globaux de l’entreprise, ce qui revient à dire que relativement aux autres sections, la taille d’une section se mesure par la masse totale des frais qu’elle supporte.

Une telle affectation des frais indirects semble harmonieuse dans la mesure où l’on ne rompt pas l’équilibre financier entre les différentes sections.

Mais il y a d’autres possibilités de mesure pour la taille d’une section.

Deuxième méthode de calcul des clés de répartition.

Cette 2ème méthode est basée sur l’hypothèse que la « taille » d’une section se mesure par le nombre d’agents affectés à cette section.

Reprenons le même exemple que précédemment et supposons que les frais directs et indirects ainsi que le personnel de l’entreprise se répartissent sur les différentes sections comme suit :

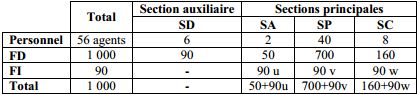
u, v et w représentent les clés de répartition (en %) des frais directs.

90 u, 90 v et 90 w représentent les frais indirects affectés respectivement aux section SA, SP et SC.

On doit avoir u + v + w = 100 %
et 90 u + 90 v + 90 w = 90

Ainsi, dire que « la taille » d’une section, relativement aux autres sections, se mesure par le nombre d’agent de cette section a pour conséquence sur la répartition des frais indirects sur les différentes sections analytiques d’être proportionnels au nombre d’agents des sections.

Traduisons alors le fait que les frais indirects de chaque section sont proportionnels au nombre d’agents de cette section.

(90 u/2) = (90 v/40 ) = (90 w / 8)

Ces deux égalités donnent une 3ème.

(90 u/2) = (90 v/40) = (90 w / 8) = (90 u + 90 v + 90 w / 2 + 40 +8)= 90/50

Et de là, nous pouvons calculer u, v, et w.

90 u/2 = 90/50

Ce qui donne u = 4 % et 90 u = 3,60

90 v/40 = 90/50

Ce qui donne v = 80 % et 90 v = 72,00

90 w/8 = 90/50

Ce qui donne w = 16 % et 90 w = 14,40

On trouve bien : u + v + w = 100 % et 90 v + 90 v + 90 w = 90

Cette 2ème méthode trouve sa justification dans le fait qu’il semble raisonnable que plus une section a d’agents plus sa « taille » est importante et plus sa « taille » est importante plus elle doit supporter une part importante des frais indirects.

Mais en ne considérant que le nombre d’agents d’une section, on occulte leur qualification ; pour ce faire une autre méthode peut être proposée.

Troisième méthode de calcul de clés de répartition.

Cette 3ème méthode est basée sur l’hypothèse que la mesure de la « taille » d’une section se mesure par la masse salariale de la section.

Reprenons le même exemple que précédemment et supposons que les frais directs et indirects ainsi que les masses salariales des différentes sections s’établissent comme suit :

a, b et c sont les clés de répartition (en %) des frais indirects.
90 a, 90 b et 90 c sont les frais indirects des 3 sections SA, SP et SC.

On doit avoir a + b + c = 100 % et 90 a + 90 b + 90 c = 90

Ainsi, dire que la « taille » d’une section, relativement aux autres sections, se mesure par la masse salariale de cette section a pour conséquence, sur la répartition des frais indirects sur les différentes sections analytiques, d’être proportionnels aux masses salariales des sections.

Traduisons le fait que les frais indirects de chaque section sont proportionnels à la masse salariale de cette section.

(90 a/40) = (90 b/340 ) = (90 c / 120)

De ces deux égalités nous pouvons déduire une 3ème.

(90 a/40) = (90 b/340 ) = (90 c / 120) = (90 ua + 90 b + 90 c / 40 + 340 + 120)= 90/500

Et de là nous pouvons calculer a, b et c.

90 a/40 = 90/500

Ce qui donne a = 8 %  et 90 a = 7,20

90 b/40 = 90/500

Ce qui donne b = 68 % et 90 b = 61,20

90 c/120 = 90/500

Ce qui donne c = 24 % et 90 c = 21,60

On trouve bien que a + b + c+ = 100 % et 90 a + 90 b + 90 c = 90

Cette 3ème méthode trouve sa justification dans le fait qu’il semble raisonnable que plus une section a d’agents qualifiés et donc une masse salariale importante, et plus cette section doit supporter de frais indirects.

Quatrième méthode de calcul des clés de répartition

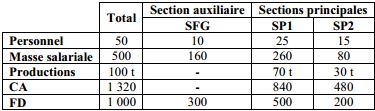
Considérons maintenant la même entreprise et supposons que sa production est faite dans deux ateliers de fabrication qui constituent deux sections analytiques homogènes principales (SP1) et (SP2) et que le reste des activités annexes de l’entreprise soit appréhendé comme une seule et même section analytique auxiliaire de frais généraux (SFG).

Le problème de la comptabilité analytique, dans ce cas, consiste à répartir les frais de la section auxiliaire des frais généraux (SFG) sur les deux autres sections principales (SP1) et (SP2).

Cette 4ème méthode est basée sur l’hypothèse que la « taille » de chaque section se mesure par le volume de production de cette section. Ce volume peut être mesuré, selon la nature des produits, en kg, m, m3, unité, etc.

Dressons le tableau des frais et des productions de chaque section.

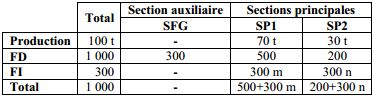
m et n sont les clés de répartition (en %) des frais indirects.

300 m et 300 n sont les frais indirects des sections SPI et SP2.
On doit avoir m + n = 100 % et 300 m + 300 n = 300.

Ainsi, dire que la « taille » d’une section, relativement aux autres sections, se mesure par le volume de production de cette section a pour conséquence sur la répartition des frais indirects des différentes sections, d’être proportionnels aux volumes de production des sections.

Traduisons alors le fait que les frais indirects des sections sont proportionnels aux productions des sections.

(300 m/70) = (300 n/30 )

De cette égalité nous déduisons une 2ème.

(300 m/70) = (300 n/30 )= (300 m +300 n / 70 + 30)= 300/100

Et de là, nous pouvons calculer m et n.

(300 m/70) =300/100

Ce qui donne m = 70 % et 300 m = 210

(300 n/30) = (300 /100 )

Ce qui donne n = 30 % et 300 n = 90

On trouve bien que m + n = 100 % et 300 m + 300 n = 300

Cette 4ème méthode trouve sa justification dans le fait qu’il semble raisonnable que plus grande est la production d’une section et plus importante doit être sa part de frais indirects à supporter.

Mais la production d’une section ne peut pas être mesurée que de façon physique (kg, m, m3, etc.). Elle peut aussi être mesurée par le chiffre d’affaires escompté en multipliant les quantités produites par les prix de vente habituels.

Cinquième méthode de calcul des clés de répartition.

Cette méthode est basée sur l’hypothèse que la « taille » d’une section analytique se mesure par le chiffre d’affaires escompté de cette section.

Reprenons le même exemple que précédemment et supposons que les frais directs et indirects ainsi que les chiffres d’affaires escomptés des différentes sections s’établissent comme suit :

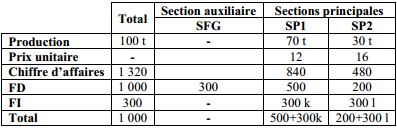
k et l sont les clés de répartition des frais indirects.
300 k et 300 l sont les frais indirects des sections SP1 et SP2.

Ainsi dire que la « taille » d’une section, relativement aux autres sections, se mesure par le volume de production de cette section a pour conséquence sur la répartition des frais indirects des différentes sections, d’être proportionnels aux volumes de production des sections.

Traduisons alors le fait que les frais indirects des sections sont proportionnels aux chiffres d’affaires de ces sections.

(300 k/840) =300 l/480

De cette égalité, nous déduisons une 2ème.

(300 k/840) =300 l/480 =(300 k +300 l)/(480+840) =300/1320

Et de là nous pourrons calculer k et l.

300 k/840 =300/1320

Ce qui donne k = 63,64 % et 300 k = 190,91

300 l/480 =300/1320

Ce qui donne l = 36,36 % et 300 l = 109,09

On trouve bien que k + l = 100 % et que 300 k + 300 l = 300

Cette 5ème méthode trouve sa justification dans le fait qu’il semble raisonnable que plus une section a un chiffre d’affaires escompté important et plus importante doit être la part de frais indirects à lui affecter.

Discussion sur les différentes méthodes de calcul.

Dressons un tableau synthétique des 5 méthodes de calcul que nous avons exposées plus haut.

Le tableau des frais indirects des différentes sections s’établit selon les méthodes :

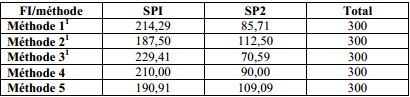
Les 5 méthodes donnent des résultats assez différents en ce sens que, par exemple, la part des frais indirects affectée à la section SP1 varie de 187,50 à 229,41 et elle est affectée à la section SP2 variant de 70,59 à 112,50.

Cette dispersion des frais indirects affectés à une section, d’une méthode à l’autre, se traduit en fait par une dispersion semblable des coûts de revient des produits P1 et P2.

Le tableau suivant donne cette dispersion des coûts de revient des produits P1 et P2 des deux sections :

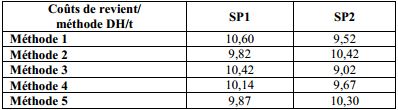
Ceci peut perturber le lecteur qui croit que les calculs des coûts et des coûts de revient sont des calculs de précision, en fait ceci doit justement montrer que les calculs des coûts et des coûts de revient doivent obéir à la politique de l’entreprise.

Il est manifeste qu’entre la méthode 3 qui charge au maximum la section SP1 et la méthode 2 qui la charge au minimum, il appartient au patron de l’entreprise et au comptable d’opter pour l’une des cinq méthodes afin de rendre le produit P1 plus ou moins rentable.

En dernier ressort, la détermination des coûts et des coûts de revient détermine le degré de rentabilité d’un produit par rapport à un autre.

Nous allons illustrer cela dans l’exemple qui suit.

Sixième méthode de calcul des clés de répartition.

Considérons toujours la même entreprise avec ses deux sections de production SP1 et SP2 et sa section de frais généraux SFG et supposons que cette entreprise envisage de lancer la production d’un 3ème produit par un 3ème atelier qui constitue la section SP3.

Dressons le tableau des frais de la nouvelle entreprise :

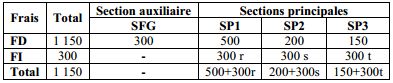
r, st et t sont les clés de répartition (en %) des frais indirects.
300 r, 300 s et 300 t sont les frais indirects affectés aux 3 sections SP1, SP2 et SP3.

Nous pouvons utiliser l’une des 5 méthodes exposées plus haut afin de calculer r, s et t, et déterminer la part des frais indirects de chaque section analytique.

Cependant comme l’entreprise est déjà rentable et qu’elle lance un nouveau produit auquel elle veut donner toutes les chances de réussite, on peut envisager que le patron de l’entreprise décide d’affecter 0 frais indirect à la section SP3. (t = 0).

Voilà une décision politique qui va permettre au produit P3 d’être sur le marché avec un coût de revient ramené aux frais directs de la section où il est produit.

Bien sûr une fois que le produit P3 est bien implanté dans le marché, la section SP3 devra supporter sa part des frais indirects de l’entreprise ce qui rendra les autres produits P1 et P2 plus rentables.

Cette dernière méthode montre, si besoin est, que la détermination des clés de répartition et en dernier ressort celle des coûts et coût de revient doit obéir à la politique de l’entreprise ; le comptable doit par conséquent opter pour une méthode qui respecte cette politique. Il peut, pour se faire, adopter l’une des cinq méthodes que nous avons explicitées plus haut ou s’en inspirer pour en proposer une autre méthode.

La panoplie des critères auxquels il peut faire référence est assez large. On peut citer à titre d’exemple :

– La surface des ateliers des sections ;
– La consommation énergétique des sections ;
– La consommation en eau des sections ;
– La consommation en matière première des sections ;
– La combinaison de plusieurs critères comme les frais directs et la consommation énergétique des sections ;
– etc.

Mais cette panoplie des critères est encore beaucoup plus large qu’on ne le pense puisqu’on peut utiliser toute combinaison de plusieurs critères.

Nous avons illustré l’exposé des méthodes présentées, plus haut, par des exemples simples qui ne peuvent couvrir l’ensemble des cas possibles pour les calculs des clés de répartition d’une entreprise.

Les exemples simples présentent l’avantage de permettre un exposé simple de la problématique essentielle de la comptabilité analytique, à savoir le calcul des clés de répartition et d’en donner quelques sections possibles.

Télécharger “Clés de répartition en comptabilité analytique” Téléchargé 790 fois – 62 Ko