La fonction de production de l’entreprise est une fonction qui relie les quantités utilisées de facteurs de production aux quantités produites. Si l’on note P, le volume de la production, K le volume de capital utilisé, et L le volume de travail nécessaire, on peut écrire : P =j(K, L). La fonction de production est aussi appelée combinaison productive, ou technologie de l’entreprise, en ce sens où elle représente toutes les combinaisons possibles de volumes de travail et de capital pem1ettant d’obtenir un niveau de production donné.
Le coût de production, ou coût total, correspond à la somme des dépenses rendues nécessaires par la production de l’ensemble des unités d’un bien au cours d’une période donnée.
La fonction de production
La fonction de production avec un facteur fixe : supposons que, à court terme, la quantité de facteur capital soit fixe, et que le producteur ne puisse faire varier que la seule quantité de facteur travail. L’évolution des quantités produites en fonction du volume de facteur travail (nombre de travailleurs) serait, par exemple, la suivante :
| Nombre de travailleurs (L) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Production (P) | 0 | 16 | 48 | 68 | 80 | 88 | 92 | 94 | 94 |
Cet exemple tient compte des hypothèses du modèle néoclassique qui seront rappelées au fur et à mesure.
La production moyenne (PM) : elle se définit par le rapport entre la production totale et la quantité de facteur travail utilisée, PM = PIL. Elle est encore appelée productivité car elle correspond à la production obtenue par unité de travail. Le calcul donne :
| Nombre de travailleurs (L) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Production Moyenne (PM) | 0 | 16 | 24 | 22.7 | 20 | 17.6 | 15.3 | 13.4 | 11.8 |
On remarque que la production moyenne croît jusqu’à un maximum puis décroît.
La productivité marginale Pm : elle correspond au supplément de production obtenu grâce à l’utilisation d’une unité supplémentaire de facteur (ici le travail), Pm =ΔP/ΔL . Le calcul donne :
| Nombre de travailleurs (L) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Production Marginale (Pm) | / | 16 | 32 | 20 | 12 | 8 | 4 | 2 | 0 |
Les auteurs néoclassiques parlent de productivité marginale décroissante, bien que celle-ci soit dans un premier temps croissante. Ce phénomène illustre le fait que la production due à la dernière unité de facteur est de moins en moins importante jusqu’a devenir nulle (malgré la multiplication du nombre de tracteurs et d’engrais, une terre ne pourra donner une récolte sans cesse croissante, l’embauche de personnes supplémentaires ne pourra faire augmenter la production si le nombre de machines est identique, etc.).
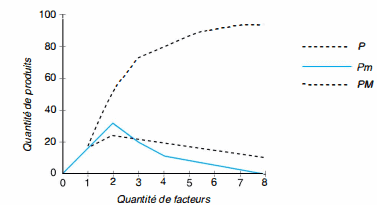
Au total, on peut dire que la production totale n’augmente pas proportionnellement à la quantité de facteur utilisée. En outre, elle n’augmente que tant que la productivité marginale est positive (on peut même imaginer une productivité marginale négative s’il y a trop de travailleurs qui finissent par se gêner). La combinaison la plus efficace se trouve au point où la productivité moyenne est maximale (2 employés, compte tenu du capital donné, produisent chacun 24 unités).
Tant que la productivité marginale est supérieure à la productivité moyenne celle-ci augmente. Lorsque la productivité marginale devient inférieure à la productivité moyenne, cette dernière diminue. Toutefois, l’entreprise peut choisir de produire plus pour des raisons stratégiques (au-delà de 48 unités) mais en acceptant une moindre productivité moyenne.
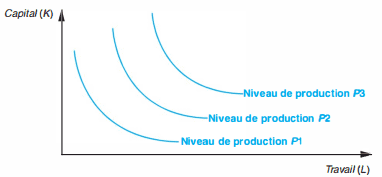
La fonction de production à facteurs substituables : elle permet de modifier la combinaison productive dans la mesure où les deux facteurs sont variables. C’est une fonction de production de long terme qui permet de faire varier le volume de capital, en sus du travail, et le volume de la production. On peut ainsi obtenir plusieurs niveaux de production (isoquantes) et, pour chacun d’eux, plusieurs combinaisons de facteurs travail et capital sont possibles. On mesure l’intensité capitalistique d’une combinaison par le coefficient de capital = KIP.
Les coûts de production
Les différents types de coûts : on distingue tout d’abord les coûts fixes, qui sont indépendants des quantités produites (amortissement, etc.) et les coûts variables qui évoluent avec le volume de la production (matières premières, etc.). La somme des coûts fixes et des coûts variables donne le coût total. Remarquons que les coûts variables peuvent être proportionnels ou non proportionnels aux quantités produites.
Le calcul des coûts : on suppose qu’une entreprise doit supporter les coûts suivants pour une production P :
| Production (P) | 1 | 2 | 3 | 4 | 5 | 6 |
| Coûts fixes (CF) | 200 | 200 | 200 | 200 | 200 | 200 |
| Coûts variables (CV) | 80 | 140 | 180 | 260 | 400 | 600 |
| Coût total (C7) | 180 | 340 | 460 | 600 | 800 |
On a : CT = CF + CV
Le coût moyen (CM) : il correspond au coût par unité produite, CM = CT/P.
Le coût marginal (Cm) : il s’agit du coût de la dernière unité produite, Cm = ΔCT/ΔP. Les calculs donnent pour CM et Cm :
| Production (P) | 1 | 2 | 3 | 4 | 5 | 6 |
| Coûts moyen (CM) | 280 | 170 | 127 | 115 | 120 | 134 |
| Coût marginale (Cm) | / | 60 | 40 | 80 | 140 | 200 |
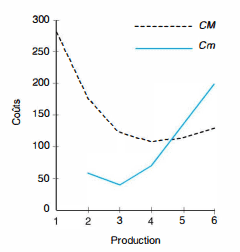
On constate que la courbe du coût marginal coupe celle du coût moyen en son minimum. Or, une entreprise continuera à produire une unité supplémentaire jusqu’à ce que le coût de cette unité (coût marginal) soit égale au prix sur le marché se situe en deçà du coût moyen (coût par unité produite), le profit de l’entreprise est négatif (prix de vente = Cm < CM). On peut en déduire que la courbe de coût marginal qui se trouve au-dessus 50 du minimum du coût moyen constitue la fonction d’offre de l’entreprise, en fonction du prix du marché.
Les économies d’échelle
Les économies d’échelle sont des économies réalisées par l’entreprise au fur et à mesure que l’on « grimpe » l’échelle de la production. On parle donc d’économies d’échelle lorsque le coût unitaire de production (coût moyen) diminue avec l’augmentation des quantités produites.
Les économies d’échelles s’expliquent par une meilleure répartition des coûts fixes sur une plus grande quantité produite, par les réductions que l’entreprise obtient sur des achats en plus grands nombre, etc.
Application : À partir des données précédentes, calculer le coût fixe moyen (CFM), CFM = CF/P. Qu’observe-t-on?
Corrigé :
| P | 1 | 2 | 3 | 4 | 5 | 6 |
| CF | 200 | 200 | 200 | 200 | 200 | 200 |
| CFM | 200 | 100 | 66 | 50 | 40 | 33 |
La diminution du coût fixe moyen illustre le phénomène des économies d’échelle. Plus les quantités produites augmentent, plus la part des coûts fixes dans le coût moyen diminue.

Sur le plan commercial, une fonction de production flexible (c’est-a-dire qui peut changer rapidement de produit fabrique) permettra de s’adapter plus rapidement aux gouts et attentes des consommateurs. L’objectif poursuivi est la minimisation du cout de production grace aux economies d’echelle et grace a la division et la specialisation des taches. Le travail est decoupe afin de produire toujours plus .