La médiane d’une variable statistique est la valeur de cette variable qui partage les effectifs supposés rangés par ordre de valeur croissante (ou décroissante) de la variable, en deux effectifs égaux. Autrement dit la médiane de x notée Med(x) est le nombre qui occupe le milieu de la distribution statistique ; elle correspond à la valeur pour laquelle la fréquence relative cumulée est égale à 1/2 ou 50% des observations.
La médiane peut être déterminée par graphique et/ou par interpolation linéaire.
N.B. Le mode de calcul de la médiane diffère selon la nature de la distribution statistique.
Calcul de la Médiane dans le cas d’une variable discrète

Pour une série d’observations individualisées ordonnées : x1, x2, x3 … , xn
on a :
• Si le nombre d’observations n est impair, c’est à dire n = 2k +1 : la médiane est unique et vaut :
![]()
Exemple: S={0 ; 1 ; 1 ; 2 ; 2 ; 3 ; 4}. La médiane est égale à Me = 2
• Si le nombre d’observations n est pair, c’est à dire n = 2k : on peut choisir approximativement comme médiane la valeur :
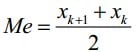
Cependant on ne peut définir qu’un intervalle médiane à l’intérieur duquel la médiane n’est pas déterminée.
Exemple : S={0 ; 0 ; 1 ; 1 ; 2 ; 2 ; 3 ; 4}. La médiane est égale à Me = (2+1)/2 = 1.5
• Lorsque les données ne sont pas individualisées, c’est à dire pour une distribution statistique ordonnée : {x1;ni}
le calcul de la médiane peut se faire via le tableau statistique, ou à partir du diagramme cumulatif tel que :
F(Med(x)) = 1/2
ou
N(Med(x)) = n/2
Trouver la Médiane à partir du tableau statistique:
On la détermine à partir des fréquence cumulées.
Remarques :
✓ Si les valeurs 0,5 ou n/2 apparaissent « entre deux lignes » du tableau. La médiane est la valeur de xi qui correspond à la ligne la plus basse des deux.
✓ On peut constater parfois que l’effectif n’est pas exactement partagé en deux sous-ensembles égaux. Cela tient au fait que l’on raisonne sur variables discrètes (voir l’exemple ci-dessous).
Exemple: Nombre d’enfants observés dans un échantillon de 55 familles
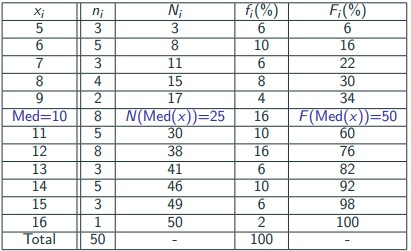
Pour cet exemple la médiane est Me = 10 (car F(Med(x)) = 50%)
• Considérons maintenant le tableau statistique qui représente la répartition du nombre d’enfants par ménage :
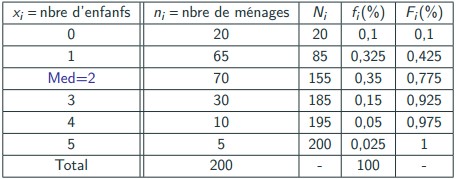
Calcul de la Médiane dans le cas d’une variable continue
Le calcul de la médiane se fait ici en deux étapes :
1. Détermination de la classe médiane : Elle se détermine, comme précédemment, à partir des colonnes des fréquences cumulées F(x) ou N(x). La règle est la même. On repère 0,5 (= 50%) dans la colonne F(x) ou n/2 dans la colonne N(x)
• Si les valeurs 0,5 ou n/2 apparaissent « entre deux lignes » du tableau : La classe médiane est celle qui correspond à la ligne la plus basse des deux.
• La détermination de la médiane (classe médiane) n’est pas affectée par des classes d’amplitudes inégales, en effet il n’est pas nécessaire, pour le calcul de la médiane, de corriger les effectifs. On ne se sert ici que des fréquences cumulées.
2. Détermination de la médiane : la Med(x) peut être déterminée par graphique et/ou par interpolation linéaire.
✓ Au niveau graphique : on se réfère au point d’intersection des courbes des fréquences cumulées descendantes et ascendantes, ou juste au point représentant 50% des effectifs sur F(x).
✓ Par interpolation linéaire : Med(x) = bi−1 +[(bi − bi−1)(50%− F(bi−1))]/[F(bi)− F(bi−1)]
ou Med(x) = bi−1 +[(bi − bi−1)(n/2− N(bi−1))]/[N(bi)− N(bi−1)]
On peut développer la méthode précédente sous une forme concise comme suit : Si ai est l’amplitude de la classe médiane, ”fi ” la fréquence relative correspondante, bi−1, la borne gauche de la classe médiane, et F (bi−1)la valeur de sa fréquence cumulée correspondante, il vient :
![]()
On prend l’exemple ci-dessous:
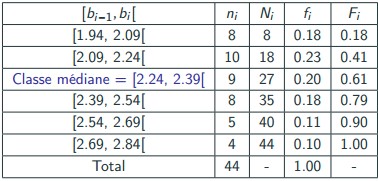
Trouver la médiane par la méthode graphique
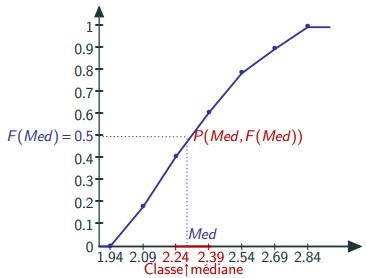
On peut calculer également la médiane soit :
✓ Par interpolation linéaire : On a la classe médiane [bi−1;bi[= [2.24;2.39[, et F(2.24) = 0.41 et F(2.39) = 0.61,
donc :Med(x) = bi−1 +[(bi −bi−1)(50%−F(bi−1))]/[F(bi)−F(bi−1)]= 2.24+[(0.15)(0.5−0.41)]/[0.61−0.41] = 2.3075
✓ Par la formule concise d’interpolation linéaire : on a l’amplitude de la classe médiane [2.24;2.39[ est ai = 0.15, sa fréquence relative est fi = 0.2, la borne gauche est bi−1 = 2.24, et la valeur de sa fréquence cumulée correspondante est F(2.24) = 0.41,
donc Med(x) = bi−1 +ai [(0,5−F(bi−1))/fi]= 2.24+0.15[ (0,5−F ( 2.24))/0.2] = 2.3075

Laisser un commentaire