Les intérêts simples : synthèse de connaissances

Les intérêts simples sont des frais que l’on paye pour l’utilisation de l’argent d’une personne ou d’une entreprise. Ils sont généralement calculés en fonction du montant emprunté et du taux d’intérêt convenu pour une période donnée. Par exemple, si vous empruntez 1 000 $ à un taux d’intérêt de 10% pendant un an, vous devrez payer 100 $ d’intérêts simples à la fin de cette période. Les intérêts simples peuvent être calculés sur une base mensuelle, trimestrielle, semestrielle ou annuelle. Il est important de noter que les intérêts simples ne tiennent pas compte du fait que les intérêts peuvent être gagnés sur les intérêts déjà accumulés. Ce concept est connu sous le nom d’intérêts composés et est généralement utilisé pour les investissements à long terme.

Ici, nous travaillons à court terme, c’est-à-dire que les intérêts sont toujours calculés sur le capital de départ et qu’ils ne sont jamais intégrés au capital. Remarque très importantes concernant ce cours sur les intérêts simples : Nous raisonnerons sur l’ensemble de ce cours résumé en temps discret (sauf celui sur la capitalisation en temps continu).

Synthèse de connaissances sur les intérêts simples

Valeur nominale : La valeur nominale d’un capitale est sa valeur à une date choisie comme date d’origine.

Intérêt : L’intérêt est le dédommagement versé au prêteur qui renonce à la satisfaction qu’il obtiendrait en dépensant immédiatement son argent.

Taux d’intérêt : Le taux d’intérêt est le loyer de l’argent. Il est égal au rapport entre le montant des intérêts obtenus et le capital placé. Une année financière comporte 360 jours. Chaque mois compte pour 30 ou 31 jours, mais il sera possible de retenir 365 jours.

REMARQUE : Dans les calculs d’intérêt, on compte le dernier jour mais pas le premier.
Par exemple, du 14/09/N au 30/10/N, il faut compter : (30 – 14) + 30 = 46 jours.

Le montant des intérêts (ou de l’escompte) est égal à :

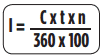
avec : C = capital ; t = taux ; n = nombre de jours

Valeur acquise

Soit un capital de valeur nominale (noté C) à une date choisie comme origine, on appelle valeur acquise par ce capital à une date postérieure à la date d’origine :

Valeur acquise = C + intérêts

Valeur actuelle et escompte

L’escompte correspond à l’intérêt prélevé par l’acquéreur d’un effet de commerce. La valeur d’un capital à une date antérieure à celle d’origine se nomme valeur actuelle :

Valeur actuelle : C – escompte

Agios

Escompte + Commissions hors taxes (fixes par effet) + TVA au taux normal.

Net porté en compte

Valeur nominale — Agios

Taux réel d’escompte

C’est le taux d’escompte réellement pratiqué par la banque ; il tient compte des agios (hors TVA) et tient compte du nombre de jours effectif.

Deux effets de commerce sont équivalents lorsqu’ils ont la même valeur actuelle. À intérêts simples, ils sont équivalents à une date et une seule.

Taux proportionnels

Des taux sont dits proportionnels quand ils sont proportionnels à la durée des périodes auxquelles ils s’appliquent. En général, nous utiliserons les taux proportionnels à intérêts simples. Avec des taux proportionnels, si l’on place deux capitaux égaux pendant le même temps, les valeurs acquises par ces capitaux sont égales.

Taux proportionnel = Taux / Nombre de périodes

[content-box color= »green »]Exemple : Calculer le taux semestriel proportionnel à un taux d’intérêt annuel de 12 %.
Le taux semestriel proportionnel est égal à : 12 % / 2 semestres = 6 %[/content-box]

Taux équivalents

Deux taux correspondant à des périodes de capitalisation différentes sont dits équivalents quand ils donnent la même valeur acquise à intérêts composés avec des capitaux égaux placés pendant la même durée totale.

[content-box color= »red »]Exemple : Calculer le taux semestriel équivalent à un taux d’intérêt annuel de 12 %.
Le taux semestriel équivalent est égal à : (1.12)^(1/2) = 5.83 %[/content-box]

Intérêts post comptés : Intérêts versés en fin de période.
Intérêts précomptés : Intérêts versés en début de période.