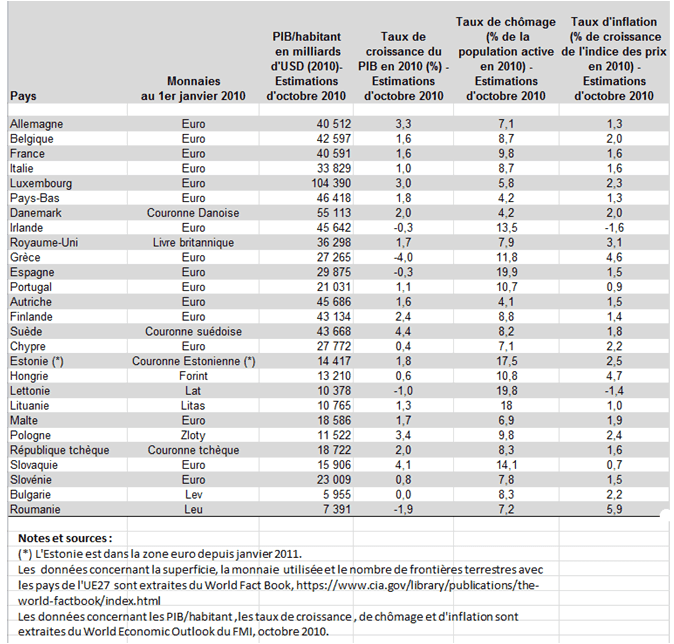
On met à votre disposition 2 TD corrigés de statistiques descriptive . Soit le tableau ci-après qui donne pour les 27 pays de l’UE, la monnaie utilisée dans ces pays au 1er janvier 2010, ainsi que les PIB/habitant en dollars, taux de croissance, de chômage et d’inflation pour l’année 2010.

TD corrigés de statistiques descriptive
Question 1 :
a) Calculer la moyenne arithmétique des taux d’inflation des 27 pays de l’UE en 2010.
b) Calculer la variance des taux d’inflation des 27 pays de l’UE en 2010. En déduire l’écart-type des taux d’inflation, ainsi que le coefficient de variation. Quel est l’intérêt de calculer le coefficient de variation ?
Question 2 :
a) Calculer la moyenne arithmétique des taux d’inflation des pays de la zone euro en 2010, puis la moyenne arithmétique des taux d’inflation des pays de l’UE 27 n’appartenant pas à la zone euro en 2010.
b) Calculer la variance des taux d’inflation des pays de la zone euro en 2010 et la variance des taux d’inflation des pays de l’UE 27 n’appartenant pas à la zone euro en 2010.
c) Décomposer la variance totale des taux d’inflation des pays de l’UE 27 entre :
- la part attribuable à la moyenne pondérée des variances des taux d’inflation de chacune des deux zones (zone euro et zone « autres monnaies de l’UE à 27 »)
- la part attribuable à la variance pondérée des moyennes des taux d’inflation de chacune des deux zones.
d) On suppose, pour l’année 2010 :
- Que tous les pays de la zone euro ont connu un taux d’inflation de 2%,
- Que tous les pays de l’UE à 27 n’appartenant pas à la zone euro ont connu un taux d’inflation de 3%.
Montrer que dans ce cas la variance totale des taux d’inflation est égale à la variance pondérée des moyennes des taux d’inflation de chaque zone.
e) On suppose, pour l’année 2010 :
- Que parmi les pays de la zone euro 8 ont eu un taux d’inflation de 1% et 8 un taux d’inflation de 2%,
- Que parmi les pays de l’UE 27 n’appartenant pas à la zone euro 3 ont eu un taux d’inflation nul, 5 un taux d’inflation de 1,5% et 3 un taux d’inflation de 3%.
Montrer que dans ce cas la variance totale des taux d’inflation de l’UE à 27 est égale à la moyenne pondérée des variances des taux d’inflation de chaque zone.
Question 3 :
a) Calculer le taux d’inflation médian des pays de l’UE 27 en 2010.
b) Déterminer l’intervalle interquartile des taux d’inflation des pays de l’UE à 27 en 2010, en utilisant la méthode de calcul employée par le tableur EXCEL (formule exposée en cours, voir la fiche « quartile et intervalle interquartile1 »).
Correction du TD de statistiques descriptive
Question 1 :
a)La moyenne arithmétique des taux d’inflation des 27 pays de la zone euro en 2010 est égale à la somme des 27 taux d’inflation, divisée par 27 : (1,3 + 2 + 1,6 + … + 2,2+6,9)/27 = 1,87 % .
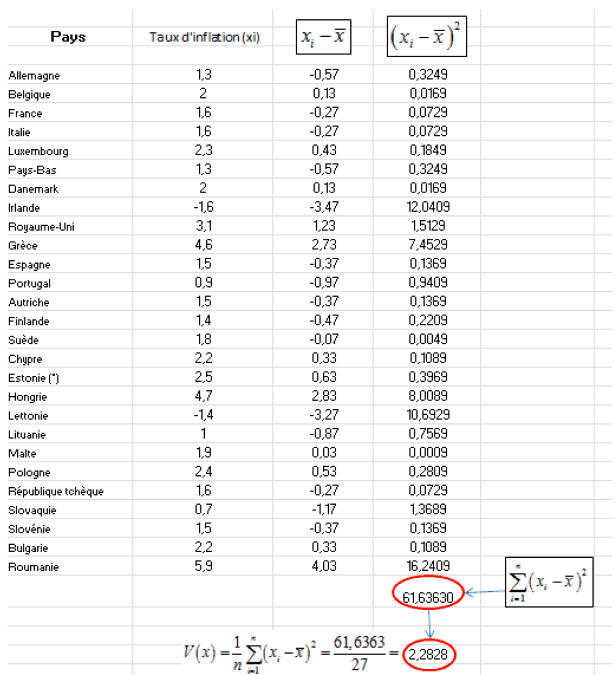
b)Soit x le symbole qui désigne le taux d’inflation et soit xi le taux d’inflation d’un pays i (avec i = 1 à 27) et soit X la moyenne arithmétique des taux d’inflation. Alors, la variance des taux d’inflation des 27 pays de l’UE est donnée par la formule :
Cette formule se calcule comme illustré dans le tableau ci-dessous :
L’écart type des taux d’inflation est égal à la racine carré de la variance, soit :
Le coefficient de variation est écart à l’écart-type divisé par la moyenne, soit (1,51/1,87)= 0,8. Le coefficient de variation est un nombre sans dimension. Il permet de comparer la dispersion des taux d’inflation avec par exemple la dispersion des taux de chômage.
Question 2 :
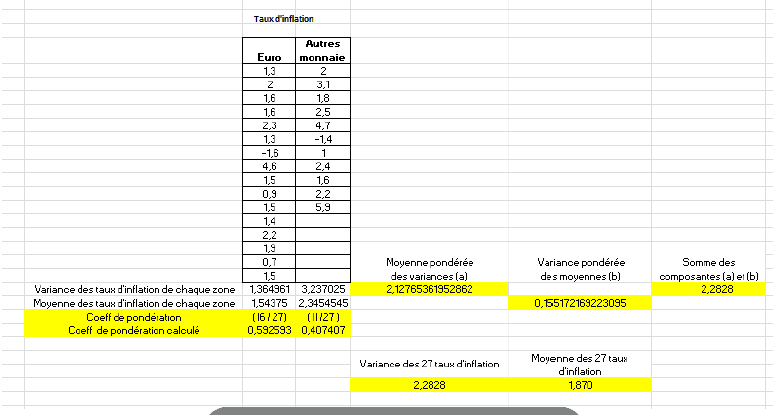
Le tableau ci-après permet de répondre aux sous-questions a), b) et c) :
a)Le tableau ci-dessus nous indique que la moyenne arithmétique des taux d’inflation des pays de la zone euro est égale à 1,54375% et celles des autres pays est égale à 2,3454545%.
b)Le tableau ci-dessus nous indique que la variance des taux d’inflation des pays de la zone euro est égale à 1,364961% et celles des autres pays est égale à 3,237025%.
c)La part attribuable à la moyenne pondérée des variances des taux d’inflation de chaque zone s’obtient par la formule suivante (en désignant par E la zone euro et par NE la zone non Euro).
(nE/n) V(E)+ (nNE/n)V(NE)
Où nE+nNE = n et où V(E) et V(NE) sont les variances des taux d’inflation dans chaque groupe de pays.
On a donc :
(16/27)* 1,364960938 + (11/27)* 3,237024793 = 2,12765361952862
La part attribuable à la variance pondérée des moyennes de taux d’inflation de chaque zone s’obtient par la formule suivante :
(nE/n) (Moyenne des taux d’inflation zone euro – moyenne des taux d’inflation UE27)2+ (nNE/n) (Moyenne du groupe des taux d’inflation zone non euro – moyenne des taux d’inflation UE27)2.
On a donc :
(16/27)(1,54375-1,87)2 + (11/27) (2,3454545-1,87)2 = 0,155172169223095
On vérifie que : 2,12765361952862 + 0,155172169223095 = 2,2828
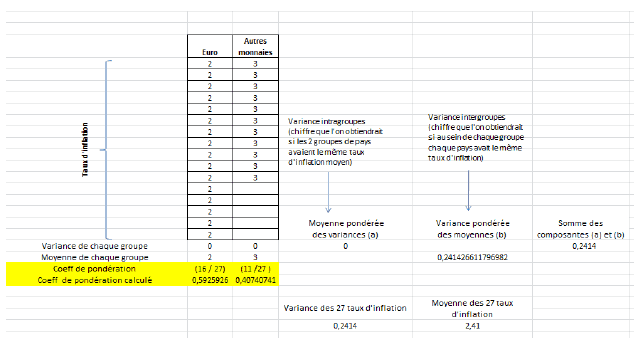
d)Le tableau ci-après concrétise cette hypothèse :
Dans ce cas, la moyenne pondérée des variances est égale à 0 et par conséquent la variance totale des taux d’inflation est égale à la variance pondérée des moyennes des taux d’inflation de chaque zone soit 0,2414.
e)Le tableau ci-après concrétise cette hypothèse :
Dans ce cas, la variance pondérée des moyennes est égale à 0 et par conséquent la variance totale des taux d’inflation de l’UE à 27 est égale à la moyenne pondérée des variances des taux d’inflation de chaque zone, soit 0,6481.
Question 3 :
a)Comme n, le nombre d’individus de la population, est impair (n=27), la médiane est égale à a (k+1) où k est défini par (n-1)/2, soit n= 2k+1 et où a (k+1) est la valeur associée à k+1.
Donc ici 27=2k+1 implique k=13 et k+1=14. Donc Me=a(k+1)=a(14)=1,6La médiane des taux de chômage est égale à 1,6%

b) Calcul de Q1, le premier quartile :
Calcul de Q3, le troisième quartile :
L’intervalle interquartile est donné par la formule :
IIQ = Q3 – Q1 = 2,25 – 1,35 = 0,9
50% des pays ont un taux d’inflation en 2010 qui est compris entre 1,35% et 2,25%.
Deuxième Td corrigé de statistique
Ces exercices de statistiques (TD) avec correction concernent les sujets suivants : Diagramme circulaire, Moyenne, médiane et quartiles, Pourcentages.
Télécharger “TD exercices statistiques” Téléchargé 1452 fois – 990 Ko

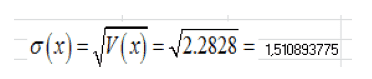



Omar
Je voudrais être formé en statistique tout en espérant que vous allez m’aider